By Anthony M. Wanjohi:
Chi square is a non-parametric test commonly used to test either goodness of fit or association between two categorical variables (test of independence). Categorical variables are grouped as nominal (names), ordinal (ordered) or dichotomous (binary). The purpose of this article is to illustrate chi square test for goodness of fit commonly used to analyze whether a frequency distribution for a categorical variable is consistent with expectations.
In order to apply the chi-square for goodness of fit test, the following are computed: Observed frequencies (Observed N), Expected frequencies (Expected N), Residual and Test Statistics.
Observed frequencies are the number of occurrences or counts, expected frequencies are the frequencies expected if the null hypothesis is true (no difference) and residual is the difference between the observed and expected frequencies (Lund Research, 2013). Test statistics provide the probability value for determination of statistical significance.
Example
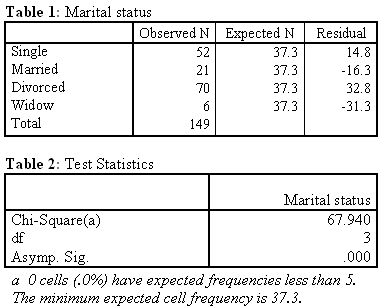
For the purpose of illustration, chi square for goodness of fit test for marital status (nominal variable) is computed. The outputs based on SPSS aided computation are shown by Tables 1 and 2.
As illustrated in Table 2, Test Statistics are statistically significant. Therefore, the null hypothesis is rejected and concluded that there is a statistical significant difference in marital status with more people being divorced as compared to single (52), married (21) and widowed (6) persons.
References
Lund Research (2013). Chi-Square Goodness-of-Fit Test in SPSS. Retrieved from https://statistics.laerd.com/spss-tutorials/chi-square-goodness-of-fit-test-in-spss-statistics.php