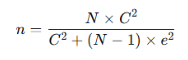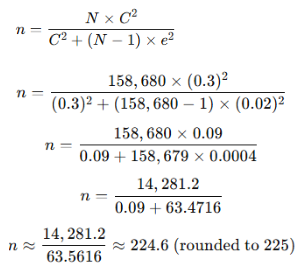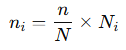Author: Anthony M. Wanjohi | Kenya Projects Organization
Corresponding Author Email: kenprokenya@gmail.com
Abstract
This article presents a systematic approach to sample size determination for known (finite) populations in quantitative research. Using Nassiuma’s formula, researchers can calculate the overall sample size based on population size, coefficient of variation, and standard error. The second step involves applying a proportional allocation formula to determine the sample sizes for individual subgroups within the population. The article uses a study of government ministries as an example to illustrate how to accurately determine sample size for a finite population.
Keywords: sample size formula, sample size determination, finite population sample size, known population sample size, proportional sample size allocation formula, population subgroups sample size determination, individual sample size, overall sample size, overall population, individual population
1. Introduction
In quantitative research, determining an appropriate sample size is a fundamental step that influences the validity, reliability, and generalizability of findings. For finite populations, where the total number of elements is known and countable, it is necessary to use formulas that account for the size of the population to avoid overestimation or underestimation of the required sample. The process generally involves two stages: determining the overall sample size using a finite population formula and then allocating that sample proportionately to subgroups within the population. This ensures precision, efficiency, and equitable representation across the study population (Nassiuma, 2000).
Step 1: Overall Sample Size Determination for a Known Population
When the total population size (N) is known, the overall sample size (n) can be calculated using Nassiuma’s (2000) finite population formula:
Where:
n = required overall sample size
N = total population size
C = coefficient of variation (commonly 21%–30%)
e = standard error (acceptable sampling error, often 2% – 5%)
The coefficient of variation (C) accounts for variability in the population, while the standard error (e) sets the allowable margin of error for estimates. This formula incorporates the finite population correction, which reduces the sample size requirement when the population is not large.
Example
In a study of staff in government ministries, the total population was N=158,680. Using C=0.3, and e=0.02, Nassiuma’s formula gives:
Thus, the total sample size required was 225 respondents.
Step 2: Individual Sample Size Determination
Once the overall sample size is known, it must be distributed among subgroups (strata) within the population in proportion to their size. This ensures that each subgroup is fairly represented in the sample. The proportional allocation formula is used:
Where:
ni = sample size for subgroup i
n = overall sample size
N = total population size
Ni = population size of subgroup i
This method ensures that larger subgroups contribute more respondents to the sample than smaller subgroups, maintaining proportionality and representativeness (Frankel & Wallen, 2000).
Example
The proportional allocation formula was applied to distribute the 225 respondents across the ministries according to their population sizes. For example:
Repeating this calculation for each ministry resulted in sample sizes that added up to the total sample of 225 respondents, ensuring proportional representation.
3. Conclusion
Sample size determination for a known population requires a structured, two-step approach: first, the computation of the overall sample size using a finite population formula, and second, proportional allocation of that sample to subgroups within the population. This method ensures statistical precision, cost efficiency, and fair representation of all subgroups. As demonstrated in the government ministries study, using Nassiuma’s (2000) formula alongside proportional allocation provides a robust framework for designing representative and efficient samples in social science research.
References
Frankel, J. R., & Wallen, N. E. (2000). How to design and evaluate research in education (4th ed.). McGraw-Hill.
Nassiuma, D. K. (2000). Survey sampling: Theory and methods. Nairobi: University of Nairobi Press.
Schmidt, N., & Brown, J. M. (2012). Evidence-based practice for nurses: Appraisal and application of research (2nd ed.). Jones & Bartlett Learning.
Teddlie, C., & Tashakkori, A. (2009). Foundations of mixed methods research: Integrating quantitative and qualitative approaches in the social and behavioral sciences. SAGE Publications.
Suggested Citation
Wanjohi, A.M. (2025). Step by Step Sample Size Determination for a Known Population Size. https://kenpro.org/papers/Step-by-Step-Sample-Size-Determination-for-a-Known-Population-Size.pdf
Download a Printer Friendly Copy in PDF Format
For research support related services, kindly Kenpro Support Team via CONTACT US